Classical Mechanics, Mathematics and Numerical background
Contents
2. Classical Mechanics, Mathematics and Numerical background¶
2.1. Introduction¶
Classical mechanics is a topic which has been taught intensively over several centuries. It is, with its many variants and ways of presenting the educational material, normally the first real physics course many of us meet and it lays the foundation for further physics studies. Many of the equations and ways of reasoning about the underlying laws of motion and pertinent forces, shape our approaches and understanding of the scientific method and discourse, as well as the way we develop our insights and deeper understanding about physical systems.
There is a wealth of well-tested (from both a physics point of view and a pedagogical standpoint) exercises and problems which can be solved analytically. However, many of these problems represent idealized and less realistic situations. The large majority of these problems are solved by paper and pencil and are traditionally aimed at what we normally refer to as continuous models from which we may find an analytical solution. As a consequence, when teaching mechanics, it implies that we can seldomly venture beyond an idealized case in order to develop our understandings and insights about the underlying forces and laws of motion.
We aim at changing this here by introducing throughout the course what we will call a computational path, where with computations we mean solving scientific problems with all possible tools and means, from plain paper an pencil exercises, via symbolic calculations to writing a code and running a program to solve a specific problem. Mathematically this normally means that we move from a continuous problem to a discretized one. This appproach enables us to solve a much broader class of problems. In mechanics this means, since we often rephrase the physical problems in terms of differential equations, that we can in most settings reuse the same program with some minimal changes.
2.2. Reminder on vectors and other mathematical quantities¶
Our studies will start with the motion of different types of objects such as a falling ball, a runner, a bicycle etc etc. It means that an object’s position in space varies with time. In order to study such systems we need to define
choice of origin
choice of the direction of the axes
choice of positive direction (left-handed or right-handed system of reference)
choice of units and dimensions
These choices lead to some important questions such as
is the physics of a system independent of the origin of the axes?
is the physics independent of the directions of the axes, that is are there privileged axes?
is the physics independent of the orientation of system?
is the physics independent of the scale of the length?
Throughout this course we will use the standardized SI units. The standard unit for length is thus one meter 1m, for mass one kilogram 1kg, for time one second 1s, for force one Newton 1kgm/s\(^2\) and for energy 1 Joule 1kgm\(^2\)s\(^{-2}\).
We will use the following notations for various variables (vectors are always boldfaced in these lecture notes):
position \(\boldsymbol{r}\), in one dimention we will normally just use \(x\),
mass \(m\),
time \(t\),
velocity \(\boldsymbol{v}\) or just \(v\) in one dimension,
acceleration \(\boldsymbol{a}\) or just \(a\) in one dimension,
momentum \(\boldsymbol{p}\) or just \(p\) in one dimension,
kinetic energy \(K\),
potential energy \(V\) and
frequency \(\omega\).
More variables will be defined as we need them.
It is also important to keep track of dimensionalities. Don’t mix this up with a chosen unit for a given variable. We mark the dimensionality in these lectures as \([a]\), where \(a\) is the quantity we are interested in. Thus
\([\boldsymbol{r}]=\) length
\([m]=\) mass
\([K]=\) energy
\([t]=\) time
\([\boldsymbol{v}]=\) length over time
\([\boldsymbol{a}]=\) length over time squared
\([\boldsymbol{p}]=\) mass times length over time
\([\omega]=\) 1/time
2.3. Scalars, Vectors and Matrices¶
A scalar is something with a value that is independent of coordinate system. Examples are mass, or the relative time between events. A vector has magnitude and direction. Under rotation, the magnitude stays the same but the direction changes. Scalars have no spatial index, whereas a three-dimensional vector has 3 indices, e.g. the position \(\boldsymbol{r}\) has components \(r_1,r_2,r_3\), which are often referred to as \(x,y,z\).
There are several categories of changes of coordinate system. The observer can translate the origin, might move with a different velocity, or might rotate her/his coordinate axes. For instance, a particle’s position vector changes when the origin is translated, but its velocity does not. When you study relativity you will find that quantities you thought of as scalars, such as time or an electric potential, are actually parts of four-dimensional vectors and that changes of the velocity of the reference frame act in a similar way to rotations.
In addition to vectors and scalars, there are matrices, which have two indices. One also has objects with 3 or four indices. These are called tensors of rank \(n\), where \(n\) is the number of indices. A matrix is a rank-two tensor. The Levi-Civita symbol, \(\epsilon_{ijk}\) used for cross products of vectors, is a tensor of rank three.
In these lectures we will use boldfaced lower-case letters to label a vector. A vector \(\boldsymbol{a}\) in three dimensions is thus defined as
and using the unit vectors (see below) in a cartesian system we have
where the unit vectors have magnitude \(\vert\boldsymbol{e}_i\vert = 1\) with \(i=1=x\), \(i=2=y\) and \(i=3=z\). Some authors use letters \(\boldsymbol{i}=\boldsymbol{e}_1\), \(\boldsymbol{j}=\boldsymbol{e}_2\) and \(\boldsymbol{k}=\boldsymbol{e}_3\).
Alternatively, you may also encounter the above vector as
Here we have used that \(a_1=a_x\), \(a_2=a_y\) and \(a_3=a_z\). Such a notation is sometimes more convenient if we wish to represent vector operations in a mathematically more compact way, see below here. We may also find this useful if we want the different components to represent other coordinate systems that the Cartesian one. A typical example would be going from a Cartesian representation to a spherical basis. We will encounter such cases many times in this course.
We use lower-case letters for vectors and upper-case letters for matrices. Vectors and matrices are always boldfaced.
2.3.1. Polar Coordinates¶
As an example, consider a two-dimensional Cartesian system with a vector \(\boldsymbol{r}=(x,y)\). Our vector is then written as
Transforming to polar coordinates with the radius \(\rho\in [0,\infty)\) and the angle \(\phi \in [0,2\pi]\) we have the familiar transformations
and the inverse relations
We can rewrite the vector \(\boldsymbol{a}\) in terms of \(\rho\) and \(\phi\) as
and we define the new unit vectors as \(\boldsymbol{e}'_1=\cos{\phi}\boldsymbol{e}_1\) and \(\boldsymbol{e}'_2=\sin{\phi}\boldsymbol{e}_2\), we have
Below we will show that the norms of this vector in a Cartesian basis and a Polar basis are equal.
2.3.2. Unit Vectors¶
Also known as basis vectors, unit vectors point in the direction of the coordinate axes, have unit norm, and are orthogonal to one another. Sometimes this is referred to as an orthonormal basis,
Here, \(\delta_{ij}\) is unity when \(i=j\) and is zero otherwise. This is called the unit matrix, because you can multiply it with any other matrix and not change the matrix. The dot denotes the dot product, \(\boldsymbol{a}\cdot\boldsymbol{b}=a_1b_1+a_2b_2+a_3b_3=|a||b|\cos\theta_{ab}\). Sometimes the unit vectors are called \(\hat{x}\), \(\hat{y}\) and \(\hat{z}\).
Vectors can be decomposed in terms of unit vectors,
The vector components \(r_1\), \(r_2\) and \(r_3\) might be called \(x\), \(y\) and \(z\) for a displacement. Another way to write this is to define the vector \(\boldsymbol{r}=(x,y,z)\).
Similarly, for the velocity we will use in this course the components \(\boldsymbol{v}=(v_x, v_y,v_z\). The accelaration is then given by \(\boldsymbol{a}=(a_x,a_y,a_z)\).
As mentioned above, repeated indices infer sums. This means that when you encounter an expression like the one on the left-hand side here, it stands actually for a sum (right-hand side)
We will in our lectures seldom use this notation and rather spell out the summations. This inferred summation over indices is normally called Einstein summation convention.
2.4. Vector Operations, Scalar Product (or dot product)¶
For two vectors \(\boldsymbol{a}\) and \(\boldsymbol{b}\) we have
or with a norm-2 notation
Not of all of you are familiar with linear algebra. Numerically we will always deal with arrays and the dot product vector is given by the product of the transposed vector multiplied with the other vector, that is we have
The superscript \(T\) represents the transposition operations.
2.5. Digression, Linear Algebra Notation for Vectors¶
As an example, consider a three-dimensional velocity defined by a vector \(\boldsymbol{v}=(v_x,v_y,v_z)\). For those of you familiar with linear algebra, we would write this quantity as
and the transpose as
The norm is
as it should.
Since we will use Python as a programming language throughout this course, the above vector, using the package numpy (see discussions below), can be written as
import numpy as np
# Define the values of vx, vy and vz
vx = 0.0
vy = 1.0
vz = 0.0
v = np.array([vx, vy, vz])
print(v)
# The print the transpose of v
print(v.T)
[0. 1. 0.]
[0. 1. 0.]
Try to figure out how to calculate the norm with numpy. We will come back to numpy in the examples below.
As an example, consider our transformation of a two-dimensional Cartesian vector \(\boldsymbol{r}\) to polar coordinates. We had
Transforming to polar coordinates with the radius \(\rho\in [0,\infty)\) and the angle \(\phi \in [0,2\pi]\) we have
We can write this
The norm in Cartesian coordinates is \(\boldsymbol{r}\cdot\boldsymbol{r}=x^2+y^2\) and using Polar coordinates we have \(\rho^2(\cos{\phi})^2+\rho^2(\cos{\phi})^2=\rho^2\), which shows that the norm is conserved since we have \(\rho = \sqrt{x^2+y^2}\). A transformation to a new basis should not change the norm.
2.6. Vector Product (or cross product) of vectors \(\boldsymbol{a}\) and \(\boldsymbol{b}\)¶
Here \(\epsilon\) is the third-rank anti-symmetric tensor, also known as the Levi-Civita symbol. It is \(\pm 1\) only if all three indices are different, and is zero otherwise. The choice of \(\pm 1\) depends on whether the indices are an even or odd permutation of the original symbols. The permutation \(xyz\) or \(123\) is considered to be \(+1\). Its elements are
You may have met cross-products when studying magnetic fields. Because the matrix is anti-symmetric, switching the \(x\) and \(y\) axes (or any two axes) flips the sign. If the coordinate system is right-handed, meaning the \(xyz\) axes satisfy \(\hat{x}\times\hat{y}=\hat{z}\), where you can point along the \(x\) axis with your extended right index finger, the \(y\) axis with your contracted middle finger and the \(z\) axis with your extended thumb. Switching to a left-handed system flips the sign of the vector \(\boldsymbol{c}=\boldsymbol{a}\times\boldsymbol{b}\).
Note that \(\boldsymbol{a}\times\boldsymbol{b}=-\boldsymbol{b}\times\boldsymbol{a}\). The vector \(\boldsymbol{c}\) is perpendicular to both \(\boldsymbol{a}\) and \(\boldsymbol{b}\) and the magnitude of \(\boldsymbol{c}\) is given by
2.6.1. Pseudo-vectors¶
Vectors obtained by the cross product of two real vectors are called pseudo-vectors because the assignment of their direction can be arbitrarily flipped by defining the Levi-Civita symbol to be based on left-handed rules. Examples are the magnetic field and angular momentum. If the direction of a real vector prefers the right-handed over the left-handed direction, that constitutes a violation of parity. For instance, one can polarize the spins (angular momentum) of nuclei with a magnetic field so that the spins preferentially point along the direction of the magnetic field. This does not violate parity because both are pseudo-vectors. Now assume these polarized nuclei decay and that electrons are one of the products. If these electrons prefer to exit the decay parallel vs. antiparallel to the polarizing magnetic field, this constitutes parity violation because the direction of the outgoing electron momenta are a real vector. This is precisely what is observed in weak decays.
2.7. Differentiation of a vector with respect to a scalar¶
As an example, consider the acceleration \(\boldsymbol{a}\), which is given by the change in velocity per unit time, \(\boldsymbol{a}=d\boldsymbol{v}/dt\) with components
Here \(i=x,y,z\) or \(i=1,2,3\) if we are in three dimensions.
2.7.1. Gradient operator \(\nabla\)¶
This represents the derivatives \(\partial/\partial x\), \(\partial/\partial y\) and \(\partial/\partial z\). An often used shorthand is \(\partial_x=\partial/\partial_x\).
The gradient of a scalar function of position and time \(\Phi(x,y,z)=\Phi(\boldsymbol{r},t)\) is given by
with components \(i\)
Note that the gradient is a vector.
Taking the dot product of the gradient with a vector, normally called the divergence, we have
Note that the divergence is a scalar.
2.7.2. The curl¶
The curl of a vector is defined as \(\nabla\times\boldsymbol{a}\),
with components
2.7.3. The Laplacian¶
The Laplacian is referred to as \(\nabla^2\) and is defined as
Question: is the Laplacian a scalar or a vector?
2.7.4. Some identities¶
Here we simply state these, but you may wish to prove a few. They are useful for this class and will be essential when you study electromagnetism.
2.7.5. More useful relations¶
Using the fact that multiplication of reals is distributive we can show that
Similarly we can also show that (using product rule for differentiating reals)
We can repeat these operations for the cross products and show that they are distribuitive
We have also that
2.7.6. Gauss’s Theorem¶
For an integral over a volume \(V\) confined by a surface \(S\), Gauss’s theorem gives
For a closed path \(C\) which carves out some area \(S\),
2.7.7. and Stokes’s Theorem¶
Stoke’s law can be understood by considering a small rectangle, \(-\Delta x<x<\Delta x\), \(-\Delta y<y<\Delta y\). The path integral around the edges is
Here \(\Delta S\) is the area of the surface element.
2.8. Basic Matrix Features¶
Note: The material on matrices is optional and will not be used much (except for illustrations at the very end on garmonic oscillations) since most of you have not yet taken a course on linear algebra. The material is however included here for the sake of completeness.
The inverse of a matrix is defined by
| Relations | Name | matrix elements |
|---|---|---|
| $A = A^{T}$ | symmetric | $a_{ij} = a_{ji}$ |
| $A = \left (A^{T} \right )^{-1}$ | real orthogonal | $\sum_k a_{ik} a_{jk} = \sum_k a_{ki} a_{kj} = \delta_{ij}$ |
| $A = A^{ * }$ | real matrix | $a_{ij} = a_{ij}^{ * }$ |
| $A = A^{\dagger}$ | hermitian | $a_{ij} = a_{ji}^{ * }$ |
| $A = \left (A^{\dagger} \right )^{-1}$ | unitary | $\sum_k a_{ik} a_{jk}^{ * } = \sum_k a_{ki}^{ * } a_{kj} = \delta_{ij}$ |
2.8.1. Some famous Matrices¶
Diagonal if \(a_{ij}=0\) for \(i\ne j\)
Upper triangular if \(a_{ij}=0\) for \(i > j\)
Lower triangular if \(a_{ij}=0\) for \(i < j\)
Upper Hessenberg if \(a_{ij}=0\) for \(i > j+1\)
Lower Hessenberg if \(a_{ij}=0\) for \(i < j+1\)
Tridiagonal if \(a_{ij}=0\) for \(|i -j| > 1\)
Lower banded with bandwidth \(p\): \(a_{ij}=0\) for \(i > j+p\)
Upper banded with bandwidth \(p\): \(a_{ij}=0\) for \(i < j+p\)
Banded, block upper triangular, block lower triangular….
For an \(N\times N\) matrix \(\mathbf{A}\) the following properties are all equivalent
If the inverse of \(\mathbf{A}\) exists, \(\mathbf{A}\) is nonsingular.
The equation \(\mathbf{Ax}=0\) implies \(\mathbf{x}=0\).
The rows of \(\mathbf{A}\) form a basis of \(R^N\).
The columns of \(\mathbf{A}\) form a basis of \(R^N\).
\(\mathbf{A}\) is a product of elementary matrices.
\(0\) is not eigenvalue of \(\mathbf{A}\).
2.9. Rotations¶
Here, we use rotations as an example of matrices and their operations. One can consider a different orthonormal basis \(\hat{e}'_1\), \(\hat{e}'_2\) and \(\hat{e}'_3\). The same vector \(\boldsymbol{r}\) mentioned above can also be expressed in the new basis,
Even though it is the same vector, the components have changed. Each new unit vector \(\hat{e}'_i\) can be expressed as a linear sum of the previous vectors,
and the matrix \(U\) can be found by taking the dot product of both sides with \(\hat{e}_k\),
Thus, the matrix lambda has components \(U_{ij}\) that are equal to the cosine of the angle between new unit vector \(\hat{e}'_i\) and the old unit vector \(\hat{e}_j\).
Note that the matrix is not symmetric, \(U_{ij}\ne U_{ji}\). One can also look at the inverse transformation, by switching the primed and unprimed coordinates,
The definition of transpose of a matrix, \(M^{t}_{ij}=M_{ji}\), allows one to state this as
2.9.1. Tensors¶
A tensor obeying Eq. (8) defines what is known as a unitary, or orthogonal, transformation.
The matrix \(U\) can be used to transform any vector to the new basis. Consider a vector
This is the same vector expressed as a sum over two different sets of basis vectors. The coefficients \(r_i\) and \(r'_i\) represent components of the same vector. The relation between them can be found by taking the dot product of each side with one of the unit vectors, \(\hat{e}_i\), which gives
Using Eq. (7) one can see that the transformation of \(r\) can be also written in terms of \(U\),
Thus, the matrix that transforms the coordinates of the unit vectors, Eq. (7) is the same one that transforms the coordinates of a vector, Eq. (9).
As a small exercise, find the rotation matrix \(U\) for finding the components in the primed coordinate system given from those in the unprimed system, given that the unit vectors in the new system are found by rotating the coordinate system by and angle \(\phi\) about the \(z\) axis.
In this case
By inspecting Eq. (5), we get
Under a unitary transformation \(U\) (or basis transformation) scalars are unchanged, whereas vectors \(\boldsymbol{r}\) and matrices \(M\) change as
Physical quantities with no spatial indices are scalars (or pseudoscalars if they depend on right-handed vs. left-handed coordinate systems), and are unchanged by unitary transformations. This includes quantities like the trace of a matrix, the matrix itself had indices but none remain after performing the trace.
Because there are no remaining indices, one expects it to be a scalar. Indeed one can see this,
A similar example is the determinant of a matrix, which is also a scalar.
2.10. Numerical Elements¶
Numerical algorithms call for approximate discrete models and much of the development of methods for continuous models are nowadays being replaced by methods for discrete models in science and industry, simply because much larger classes of problems can be addressed with discrete models, often by simpler and more generic methodologies.
As we will see throughout this course, when properly scaling the equations at hand, discrete models open up for more advanced abstractions and the possibility to study real life systems, with the added bonus that we can explore and deepen our basic understanding of various physical systems
Analytical solutions are as important as before. In addition, such solutions provide us with invaluable benchmarks and tests for our discrete models. Such benchmarks, as we will see below, allow us to discuss possible sources of errors and their behaviors. And finally, since most of our models are based on various algorithms from numerical mathematics, we have a unique oppotunity to gain a deeper understanding of the mathematical approaches we are using.
With computing and data science as important elements in essentially all aspects of a modern society, we could then try to define Computing as solving scientific problems using all possible tools, including symbolic computing, computers and numerical algorithms, and analytical paper and pencil solutions. Computing provides us with the tools to develope our own understanding of the scientific method by enhancing algorithmic thinking.
The way we will teach this course reflects this definition of computing. The course contains both classical paper and pencil exercises as well as computational projects and exercises. The hope is that this will allow you to explore the physics of systems governed by the degrees of freedom of classical mechanics at a deeper level, and that these insights about the scientific method will help you to develop a better understanding of how the underlying forces and equations of motion and how they impact a given system.
Furthermore, by introducing various numerical methods via computational projects and exercises, we aim at developing your competences and skills about these topics.
These competences will enable you to
understand how algorithms are used to solve mathematical problems,
derive, verify, and implement algorithms,
understand what can go wrong with algorithms,
use these algorithms to construct reproducible scientific outcomes and to engage in science in ethical ways, and
think algorithmically for the purposes of gaining deeper insights about scientific problems.
All these elements are central for maturing and gaining a better understanding of the modern scientific process per se.
The power of the scientific method lies in identifying a given problem as a special case of an abstract class of problems, identifying general solution methods for this class of problems, and applying a general method to the specific problem (applying means, in the case of computing, calculations by pen and paper, symbolic computing, or numerical computing by ready-made and/or self-written software). This generic view on problems and methods is particularly important for understanding how to apply available, generic software to solve a particular problem.
However, verification of algorithms and understanding their limitations requires much of the classical knowledge about continuous models.
2.11. A well-known example to illustrate many of the above concepts¶
Before we venture into a reminder on Python and mechanics relevant applications, let us briefly outline some of the abovementioned topics using an example many of you may have seen before in for example CMSE201. A simple algorithm for integration is the Trapezoidal rule. Integration of a function \(f(x)\) by the Trapezoidal Rule is given by following algorithm for an interval \(x \in [a,b]\)
where \(h\) is the so-called stepsize defined by the number of integration points \(N\) as \(h=(b-a)/(n)\). Python offers an extremely versatile programming environment, allowing for the inclusion of analytical studies in a numerical program. Here we show an example code with the trapezoidal rule. We use also SymPy to evaluate the exact value of the integral and compute the absolute error with respect to the numerically evaluated one of the integral \(\int_0^1 dx x^2 = 1/3\). The following code for the trapezoidal rule allows you to plot the relative error by comparing with the exact result. By increasing to \(10^8\) points one arrives at a region where numerical errors start to accumulate.
%matplotlib inline
from math import log10
import numpy as np
from sympy import Symbol, integrate
import matplotlib.pyplot as plt
# function for the trapezoidal rule
def Trapez(a,b,f,n):
h = (b-a)/float(n)
s = 0
x = a
for i in range(1,n,1):
x = x+h
s = s+ f(x)
s = 0.5*(f(a)+f(b)) +s
return h*s
# function to compute pi
def function(x):
return x*x
# define integration limits
a = 0.0; b = 1.0;
# find result from sympy
# define x as a symbol to be used by sympy
x = Symbol('x')
exact = integrate(function(x), (x, a, b))
# set up the arrays for plotting the relative error
n = np.zeros(9); y = np.zeros(9);
# find the relative error as function of integration points
for i in range(1, 8, 1):
npts = 10**i
result = Trapez(a,b,function,npts)
RelativeError = abs((exact-result)/exact)
n[i] = log10(npts); y[i] = log10(RelativeError);
plt.plot(n,y, 'ro')
plt.xlabel('n')
plt.ylabel('Relative error')
plt.show()
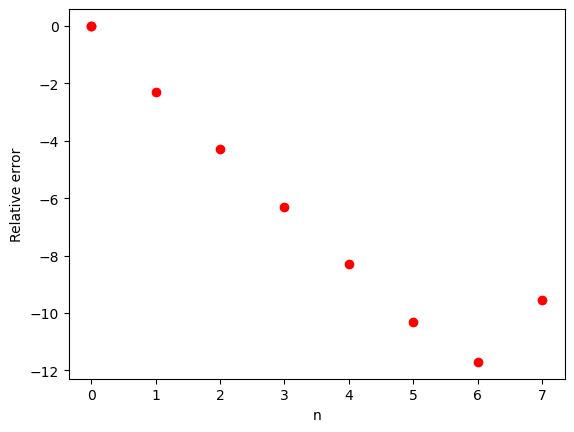
2.11.1. Analyzing the above example¶
This example shows the potential of combining numerical algorithms with symbolic calculations, allowing us to
Validate and verify their algorithms.
Including concepts like unit testing, one has the possibility to test and test several or all parts of the code.
Validation and verification are then included naturally and one can develop a better attitude to what is meant with an ethically sound scientific approach.
The above example allows the student to also test the mathematical error of the algorithm for the trapezoidal rule by changing the number of integration points. The students get trained from day one to think error analysis.
With a Jupyter notebook you can keep exploring similar examples and turn them in as your own notebooks.
2.12. Python practicalities, Software and needed installations¶
We will make extensive use of Python as programming language and its myriad of available libraries. You will find Jupyter notebooks invaluable in your work.
If you have Python installed (we strongly recommend Python3) and you feel pretty familiar with installing different packages, we recommend that you install the following Python packages via pip as
pip install numpy scipy matplotlib ipython scikit-learn mglearn sympy pandas pillow
For Python3, replace pip with pip3.
For OSX users we recommend, after having installed Xcode, to install brew. Brew allows for a seamless installation of additional software via for example
brew install python3
For Linux users, with its variety of distributions like for example the widely popular Ubuntu distribution, you can use pip as well and simply install Python as
sudo apt-get install python3 (or python for pyhton2.7)
etc etc.
2.12.1. Python installers¶
If you don’t want to perform these operations separately and venture into the hassle of exploring how to set up dependencies and paths, we recommend two widely used distrubutions which set up all relevant dependencies for Python, namely
which is an open source distribution of the Python and R programming languages for large-scale data processing, predictive analytics, and scientific computing, that aims to simplify package management and deployment. Package versions are managed by the package management system conda.
is a Python distribution for scientific and analytic computing distribution and analysis environment, available for free and under a commercial license.
Furthermore, Google’s Colab is a free Jupyter notebook environment that requires no setup and runs entirely in the cloud. Try it out!
2.13. Useful Python libraries¶
Here we list several useful Python libraries we strongly recommend (if you use anaconda many of these are already there)
NumPy is a highly popular library for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays
The pandas library provides high-performance, easy-to-use data structures and data analysis tools
Xarray is a Python package that makes working with labelled multi-dimensional arrays simple, efficient, and fun!
Scipy (pronounced “Sigh Pie”) is a Python-based ecosystem of open-source software for mathematics, science, and engineering.
Matplotlib is a Python 2D plotting library which produces publication quality figures in a variety of hardcopy formats and interactive environments across platforms.
Autograd can automatically differentiate native Python and Numpy code. It can handle a large subset of Python’s features, including loops, ifs, recursion and closures, and it can even take derivatives of derivatives of derivatives
SymPy is a Python library for symbolic mathematics.
scikit-learn has simple and efficient tools for machine learning, data mining and data analysis
TensorFlow is a Python library for fast numerical computing created and released by Google
Keras is a high-level neural networks API, written in Python and capable of running on top of TensorFlow, CNTK, or Theano
Your jupyter notebook can easily be converted into a nicely rendered PDF file or a Latex file for further processing. For example, convert to latex as
pycod jupyter nbconvert filename.ipynb --to latex
And to add more versatility, the Python package SymPy is a Python library for symbolic mathematics. It aims to become a full-featured computer algebra system (CAS) and is entirely written in Python.
2.14. Numpy examples and Important Matrix and vector handling packages¶
There are several central software libraries for linear algebra and eigenvalue problems. Several of the more popular ones have been wrapped into ofter software packages like those from the widely used text Numerical Recipes. The original source codes in many of the available packages are often taken from the widely used software package LAPACK, which follows two other popular packages developed in the 1970s, namely EISPACK and LINPACK. We describe them shortly here.
LINPACK: package for linear equations and least square problems.
LAPACK:package for solving symmetric, unsymmetric and generalized eigenvalue problems. From LAPACK’s website http://www.netlib.org it is possible to download for free all source codes from this library. Both C/C++ and Fortran versions are available.
BLAS (I, II and III): (Basic Linear Algebra Subprograms) are routines that provide standard building blocks for performing basic vector and matrix operations. Blas I is vector operations, II vector-matrix operations and III matrix-matrix operations. Highly parallelized and efficient codes, all available for download from http://www.netlib.org.
Numpy provides an easy way to handle arrays in Python. The standard way to import this library is as
import numpy as np
Here follows a simple example where we set up an array of ten elements, all determined by random numbers drawn according to the normal distribution,
n = 10
x = np.random.normal(size=n)
print(x)
[-1.83408226 -0.4118334 -1.21071409 -0.59684054 0.70333963 0.0289105
0.75626664 -1.48393448 0.76111648 0.37006943]
We defined a vector \(x\) with \(n=10\) elements with its values given by the Normal distribution \(N(0,1)\). Another alternative is to declare a vector as follows
import numpy as np
x = np.array([1, 2, 3])
print(x)
[1 2 3]
Here we have defined a vector with three elements, with \(x_0=1\), \(x_1=2\) and \(x_2=3\). Note that both Python and C++ start numbering array elements from \(0\) and on. This means that a vector with \(n\) elements has a sequence of entities \(x_0, x_1, x_2, \dots, x_{n-1}\). We could also let (recommended) Numpy to compute the logarithms of a specific array as
import numpy as np
x = np.log(np.array([4, 7, 8]))
print(x)
[1.38629436 1.94591015 2.07944154]
In the last example we used Numpy’s unary function \(np.log\). This function is highly tuned to compute array elements since the code is vectorized and does not require looping. We normaly recommend that you use the Numpy intrinsic functions instead of the corresponding log function from Python’s math module. The looping is done explicitely by the np.log function. The alternative, and slower way to compute the logarithms of a vector would be to write
import numpy as np
from math import log
x = np.array([4, 7, 8])
for i in range(0, len(x)):
x[i] = log(x[i])
print(x)
[1 1 2]
We note that our code is much longer already and we need to import the log function from the math module. The attentive reader will also notice that the output is \([1, 1, 2]\). Python interprets automagically our numbers as integers (like the automatic keyword in C++). To change this we could define our array elements to be double precision numbers as
import numpy as np
x = np.log(np.array([4, 7, 8], dtype = np.float64))
print(x)
[1.38629436 1.94591015 2.07944154]
or simply write them as double precision numbers (Python uses 64 bits as default for floating point type variables), that is
import numpy as np
x = np.log(np.array([4.0, 7.0, 8.0])
print(x)
Input In [9]
print(x)
^
SyntaxError: invalid syntax
To check the number of bytes (remember that one byte contains eight bits for double precision variables), you can use simple use the itemsize functionality (the array \(x\) is actually an object which inherits the functionalities defined in Numpy) as
import numpy as np
x = np.log(np.array([4.0, 7.0, 8.0])
print(x.itemsize)
2.14.1. Matrices in Python¶
Having defined vectors, we are now ready to try out matrices. We can define a \(3 \times 3 \) real matrix \(\hat{A}\) as (recall that we user lowercase letters for vectors and uppercase letters for matrices)
import numpy as np
A = np.log(np.array([ [4.0, 7.0, 8.0], [3.0, 10.0, 11.0], [4.0, 5.0, 7.0] ]))
print(A)
If we use the shape function we would get \((3, 3)\) as output, that is verifying that our matrix is a \(3\times 3\) matrix. We can slice the matrix and print for example the first column (Python organized matrix elements in a row-major order, see below) as
import numpy as np
A = np.log(np.array([ [4.0, 7.0, 8.0], [3.0, 10.0, 11.0], [4.0, 5.0, 7.0] ]))
# print the first column, row-major order and elements start with 0
print(A[:,0])
We can continue this was by printing out other columns or rows. The example here prints out the second column
import numpy as np
A = np.log(np.array([ [4.0, 7.0, 8.0], [3.0, 10.0, 11.0], [4.0, 5.0, 7.0] ]))
# print the first column, row-major order and elements start with 0
print(A[1,:])
Numpy contains many other functionalities that allow us to slice, subdivide etc etc arrays. We strongly recommend that you look up the Numpy website for more details. Useful functions when defining a matrix are the np.zeros function which declares a matrix of a given dimension and sets all elements to zero
import numpy as np
n = 10
# define a matrix of dimension 10 x 10 and set all elements to zero
A = np.zeros( (n, n) )
print(A)
or initializing all elements to
import numpy as np
n = 10
# define a matrix of dimension 10 x 10 and set all elements to one
A = np.ones( (n, n) )
print(A)
or as unitarily distributed random numbers (see the material on random number generators in the statistics part)
import numpy as np
n = 10
# define a matrix of dimension 10 x 10 and set all elements to random numbers with x \in [0, 1]
A = np.random.rand(n, n)
print(A)
2.14.2. Meet the Pandas¶
Another useful Python package is pandas, which is an open source library providing high-performance, easy-to-use data structures and data analysis tools for Python. pandas stands for panel data, a term borrowed from econometrics and is an efficient library for data analysis with an emphasis on tabular data.
pandas has two major classes, the DataFrame class with two-dimensional data objects and tabular data organized in columns and the class Series with a focus on one-dimensional data objects. Both classes allow you to index data easily as we will see in the examples below. pandas allows you also to perform mathematical operations on the data, spanning from simple reshapings of vectors and matrices to statistical operations.
The following simple example shows how we can, in an easy way make tables of our data. Here we define a data set which includes names, place of birth and date of birth, and displays the data in an easy to read way. We will see repeated use of pandas, in particular in connection with classification of data.
import pandas as pd
from IPython.display import display
data = {'First Name': ["Frodo", "Bilbo", "Aragorn II", "Samwise"],
'Last Name': ["Baggins", "Baggins","Elessar","Gamgee"],
'Place of birth': ["Shire", "Shire", "Eriador", "Shire"],
'Date of Birth T.A.': [2968, 2890, 2931, 2980]
}
data_pandas = pd.DataFrame(data)
display(data_pandas)
In the above we have imported pandas with the shorthand pd, the latter has become the standard way we import pandas. We make then a list of various variables and reorganize the above lists into a DataFrame and then print out a neat table with specific column labels as Name, place of birth and date of birth. Displaying these results, we see that the indices are given by the default numbers from zero to three. pandas is extremely flexible and we can easily change the above indices by defining a new type of indexing as
data_pandas = pd.DataFrame(data,index=['Frodo','Bilbo','Aragorn','Sam'])
display(data_pandas)
Thereafter we display the content of the row which begins with the index Aragorn
display(data_pandas.loc['Aragorn'])
We can easily append data to this, for example
new_hobbit = {'First Name': ["Peregrin"],
'Last Name': ["Took"],
'Place of birth': ["Shire"],
'Date of Birth T.A.': [2990]
}
data_pandas=data_pandas.append(pd.DataFrame(new_hobbit, index=['Pippin']))
display(data_pandas)
Here are other examples where we use the DataFrame functionality to handle arrays, now with more interesting features for us, namely numbers. We set up a matrix of dimensionality \(10\times 5\) and compute the mean value and standard deviation of each column. Similarly, we can perform mathematial operations like squaring the matrix elements and many other operations.
import numpy as np
import pandas as pd
from IPython.display import display
np.random.seed(100)
# setting up a 10 x 5 matrix
rows = 10
cols = 5
a = np.random.randn(rows,cols)
df = pd.DataFrame(a)
display(df)
print(df.mean())
print(df.std())
display(df**2)
Thereafter we can select specific columns only and plot final results
df.columns = ['First', 'Second', 'Third', 'Fourth', 'Fifth']
df.index = np.arange(10)
display(df)
print(df['Second'].mean() )
print(df.info())
print(df.describe())
from pylab import plt, mpl
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
df.cumsum().plot(lw=2.0, figsize=(10,6))
plt.show()
df.plot.bar(figsize=(10,6), rot=15)
plt.show()
We can produce a \(4\times 4\) matrix
b = np.arange(16).reshape((4,4))
print(b)
df1 = pd.DataFrame(b)
print(df1)
and many other operations.
The Series class is another important class included in pandas. You can view it as a specialization of DataFrame but where we have just a single column of data. It shares many of the same features as DataFrame. As with DataFrame, most operations are vectorized, achieving thereby a high performance when dealing with computations of arrays, in particular labeled arrays. As we will see below it leads also to a very concice code close to the mathematical operations we may be interested in. For multidimensional arrays, we recommend strongly xarray. xarray has much of the same flexibility as pandas, but allows for the extension to higher dimensions than two.
2.15. Introduction to Git and GitHub/GitLab and similar¶
Git is a distributed version-control system for tracking changes in any set of files, originally designed for coordinating work among programmers cooperating on source code during software development.
The reference document and videos here give you an excellent introduction to the git.
We believe you will find version-control software very useful in your work.
All teaching material related to this course is open and freely available via the GitHub site of the course. The video here gives a short intro to GitHub.
See also the overview video on Git and GitHub.
2.15.1. Useful Git and GitHub links¶
These are a couple references that we have found useful (git commands, markdown, GitPages):
When dealing with homeworks, at some point you would need to use an editor, or an integrated development envinroment (IDE). As an IDE, we would like to recommend anaconda since we end up using jupyter-notebooks. anaconda runs on all known operating systems.
If you prefer editing Python codes, there are several excellent cross-platform editors. If you are in a Windows environment, word is the classical text editor.
There is however a wealth of text editors and/ord IDEs that run on all operating systems and functions well with Python. Some of the more popular ones are
